
Το Τμήμα Μαθηματικών του Πανεπιστημίου Πατρών διατηρεί μια παράδοση προσέλκυσης εξαίρετων φοιτητών, στους οποίους προσφέρει υψηλής ποιότητας σπουδές στην επιστήμη των μαθηματικών. H εκπαίδευση των φοιτητών μας βασίζεται στο τετραετές πρόγραμμα προπτυχιακών σπουδών (8 ακαδημαϊκά εξάμηνα) που απαρτίζεται από δύο περιόδους. Η πρώτη περίοδος (κορμός) έχει διάρκεια 5 εξάμηνα και προσφέρει ένα βασικό πυρήνα μαθηματικών γνώσεων μέσω υποχρεωτικών μαθημάτων. Στη δεύτερη περίοδο, διάρκειας 3 εξαμήνων, θεματικά συγγενή μαθήματα οργανώνονται και συνδυάζονται σε μια συμπαγή επιστημονική και εκπαιδευτική ενότητα προκειμένου να συγκροτήσουν μία από τις προσφερόμενες πέντε κατευθύνσεις σπουδών:
- Θεωρητικά Μαθηματικά,
- Εφαρμοσμένα Μαθηματικά,
- Πληροφορική και Υπολογιστικά Μαθηματικά,
- Στατιστική – Θεωρία Πιθανοτήτων και Επιχειρησιακή Έρευνα,
- Γενική.
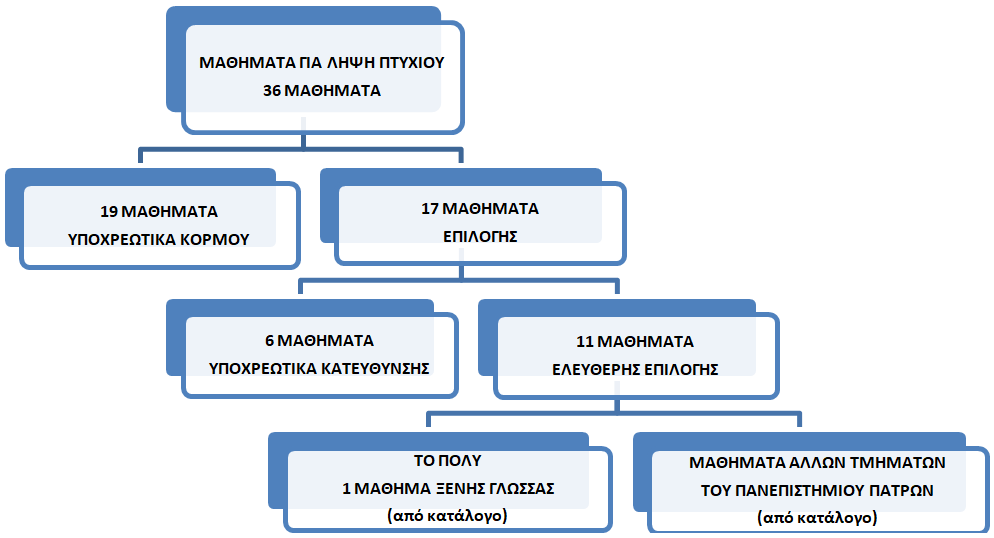
Το σύστημα επιλογής κατεύθυνσης για εμβάθυνση στις σπουδές, γίνεται σε τρόπο ώστε οι φοιτητές να έχουν μεγάλα περιθώρια για προσωπική επιλογή και διαμόρφωση του προγράμματος σπουδών τους σύμφωνα με τα ειδικά ενδιαφέροντά τους σε κάποια από τις πολυποίκιλες πτυχές ή εφαρμογές της μαθηματικής επιστήμης. Με δεδομένη τη στρατηγική απόφαση για ενιαίο πτυχίο και τη σημερινή φυσιογνωμία του Τμήματος, το ισχύον πρόγραμμα σπουδών εξασφαλίζει:
- τη διατήρηση ενός ισχυρού κορμού 19 μαθημάτων που είναι υποχρεωμένο το 100% των φοιτητών ενός μαθηματικού τμήματος να κατέχει πλήρως,
- την ευελιξία στην επιλογή 17 επιπλέον μαθημάτων ανάλογα με την προτιμώμενη κατεύθυνση σπουδών και τον προσανατολισμό των φοιτητών σε περαιτέρω εξειδίκευση.
Η εκπαίδευση των φοιτητών του Τμήματός μας γίνεται με παραδόσεις μαθημάτων, ασκήσεις, εκπονήσεις εργασιών, σεμινάρια, μελέτες περιπτώσεων, κ.λπ. Τα μαθήματα έχουν θεωρητικό αλλά και φροντιστηριακό/εργαστηριακό μέρος. Οι φροντιστηριακές/εργαστηριακές ασκήσεις δεν είναι αυτοτελή μαθήματα, αλλά συμπληρώνουν τη διδασκαλία κάθε μαθήματος, με την εμπέδωση της ύλης, που έχει διδαχθεί και την πρακτική εφαρμογή των γνώσεων που έχουν αποκτηθεί από τις παραδόσεις. Τα φροντιστήρια και εργαστήρια διεξάγονται σε ολιγομελείς ομάδες φοιτητών, γεγονός που επιτρέπει την ενεργητική συμμετοχή τους σε αυτά.
Περισσότερες πληροφορίες σε σχέση με το πρόγραμμα σπουδών παρέχονται στον Οδηγό Σπουδών του τμήματος. Η τελευταία αναθεώρηση του προγράμματος προπτυχιακών σπουδών πραγματοποιήθηκε το ακαδημαϊκό έτος 2013-2014, με τις κατευθύνσεις, να διαμορφώνονται στη σημερινή (οριστική) τους δομή, το 2016-2017. Όλοι οι φοιτητές μας ακολουθούν το ίδιο πρόγραμμα σπουδών, ανεξάρτητα του έτους εισαγωγής τους (αν και ισχύουν μεταβατικές διατάξεις διευκόλυνσης για τους φοιτητές των παλαιότερων ετών).